Đạo hàm giá trị tuyệt đối: Phương pháp tiếp cận toàn diện
I. Giới thiệu
Đạo hàm của hàm giá trị tuyệt đối là một trong những chủ đề quan trọng trong chương trình Giải tích. Việc hiểu rõ và nắm vững cách tính đạo hàm của hàm số chứa giá trị tuyệt đối không chỉ giúp học sinh giải được nhiều dạng bài tập mà còn là nền tảng để tiếp cận các khái niệm phức tạp hơn trong toán học.

II. Kiến thức cơ bản
1. Định nghĩa giá trị tuyệt đối
Giá trị tuyệt đối của một số thực x, ký hiệu |x|, được định nghĩa như sau:
- |x| = x nếu x ≥ 0
- |x| = -x nếu x < 0
2. Tính chất của hàm giá trị tuyệt đối
a) |x| ≥ 0 với mọi x ∈ R
b) |x| = 0 ⟺ x = 0
c) |xy| = |x|.|y|
d) |x + y| ≤ |x| + |y|
III. Đạo hàm của hàm giá trị tuyệt đối
1. Công thức tổng quát
Cho hàm số f(x) = |u(x)|, trong đó u(x) là một hàm số khả vi tại x₀, ta có:
f'(x₀) = u'(x₀).sgn(u(x₀))
Trong đó: sgn(x) là hàm dấu, được định nghĩa:
- sgn(x) = 1 khi x > 0
- sgn(x) = -1 khi x < 0
- sgn(x) không xác định khi x = 0
2. Các trường hợp đặc biệt
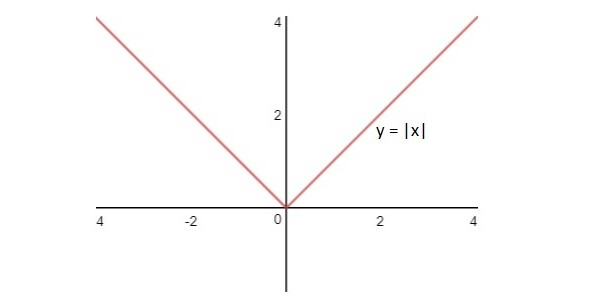
a) f(x) = |x|
- f'(x) = 1 khi x > 0
- f'(x) = -1 khi x < 0
- f'(x) không xác định tại x = 0
b) f(x) = |ax + b|
- f'(x) = a khi ax + b > 0
- f'(x) = -a khi ax + b < 0
- f'(x) không xác định khi ax + b = 0
IV. Phương pháp giải bài tập
1. Các bước cơ bản
- Xác định biểu thức trong dấu giá trị tuyệt đối
- Tìm điểm mà biểu thức trong dấu giá trị tuyệt đối bằng 0
- Chia miền xác định thành các khoảng
- Tính đạo hàm trên từng khoảng
- Kết hợp các kết quả
2. Ví dụ minh họa
Ví dụ 1: Tính đạo hàm của f(x) = |2x – 3|
Lời giải:
- Biểu thức trong dấu giá trị tuyệt đối: u(x) = 2x – 3
- Điểm u(x) = 0 ⟺ 2x – 3 = 0 ⟺ x = 3/2
- Chia miền xác định:
- Khi x < 3/2: f'(x) = -2
- Khi x > 3/2: f'(x) = 2
- Tại x = 3/2: f'(x) không xác định
Ví dụ 2: Tính đạo hàm của f(x) = x|x|
Lời giải:
- f(x) = x² khi x ≥ 0
- f(x) = -x² khi x < 0
- Do đó:
- Khi x > 0: f'(x) = 2x
- Khi x < 0: f'(x) = -2x
- Tại x = 0: f'(x) = 0

V. Các dạng bài tập thường gặp
1. Tìm đạo hàm của hàm số chứa giá trị tuyệt đối
2. Tìm tiệm cận của hàm số chứa giá trị tuyệt đối
3. Khảo sát sự biến thiên của hàm số chứa giá trị tuyệt đối
4. Tìm cực trị của hàm số chứa giá trị tuyệt đối
VI. Mẹo và lưu ý quan trọng
- Luôn xác định rõ điểm mà biểu thức trong dấu giá trị tuyệt đối bằng 0
- Chú ý tính liên tục của hàm số tại các điểm “gãy”
- Khi khảo sát đồ thị, cần đặc biệt chú ý các điểm mà đạo hàm không xác định
- Kiểm tra kỹ các điều kiện xác định của hàm số
VII. Ứng dụng thực tế
- Trong vật lý: Tính toán quãng đường trong chuyển động
- Trong kinh tế: Phân tích biến động giá cả
- Trong kỹ thuật: Tính toán sai số và dung sai
VIII. Kết luận
Đạo hàm của hàm giá trị tuyệt đối là một chủ đề quan trọng trong chương trình Giải tích. Việc nắm vững kiến thức này sẽ giúp học sinh:
- Phát triển tư duy logic và khả năng phân tích
- Giải quyết được nhiều bài toán phức tạp
- Có nền tảng vững chắc cho các môn học nâng cao
IX. Bài tập tự luyện
- Tính đạo hàm của f(x) = |x² – 1|
- Tìm điểm cực trị của f(x) = |x – 1| + |x + 1|
- Khảo sát sự biến thiên của f(x) = x|x – 2|
Để được tư vấn và hỗ trợ thêm về môn Toán cũng như các môn học khác, vui lòng liên hệ:
Trung Tâm Gia sư IJSER
- Hotline: 0909 223 113
- Email: [email protected]
- Website: ijsernet.org
Trung tâm Gia sư IJSER tự hào là đơn vị cung cấp dịch vụ gia sư uy tín, chất lượng với đội ngũ giáo viên giàu kinh nghiệm, tận tâm. Chúng tôi cam kết mang đến cho học sinh những kiến thức nền tảng vững chắc và phương pháp học tập hiệu quả.